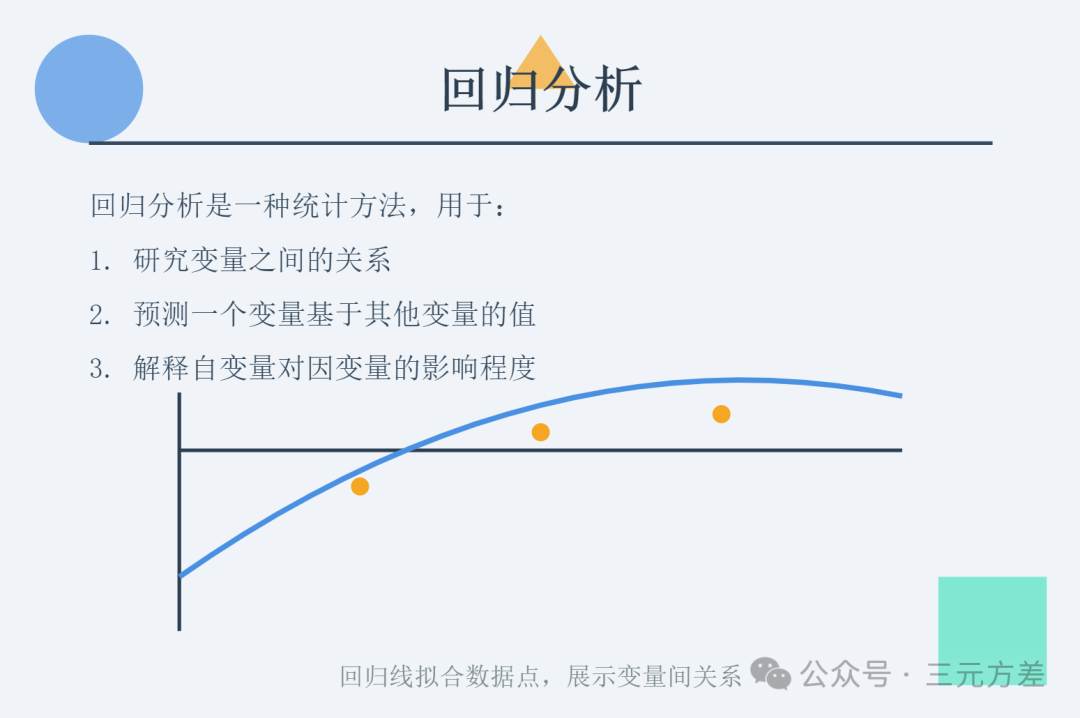
今天聊一聊预测常用的分析方法——回归分析。
想象一下，你是一名出租车司机。每天接单的数量不同，赚到的钱自然也不一样。
有一天，你突发奇想：能不能根据接单数预测一天能赚多少钱呢？
这就是回归分析要解决的问题。
它帮你找出变量之间的关系，比如接单数（自变量）和收入（因变量）之间的关系。
"回归"这个词，其实是在说我们要回到数据的本源，找出其中的规律。
1. 线性回归：一条直线背后的商业洞察
上一篇，我们探讨了相关性。
相关性，能知道两件事情是否有关。
在此基础上，回归分析可以帮助我们更进一步，知道A没变动一点，B会变动多少。
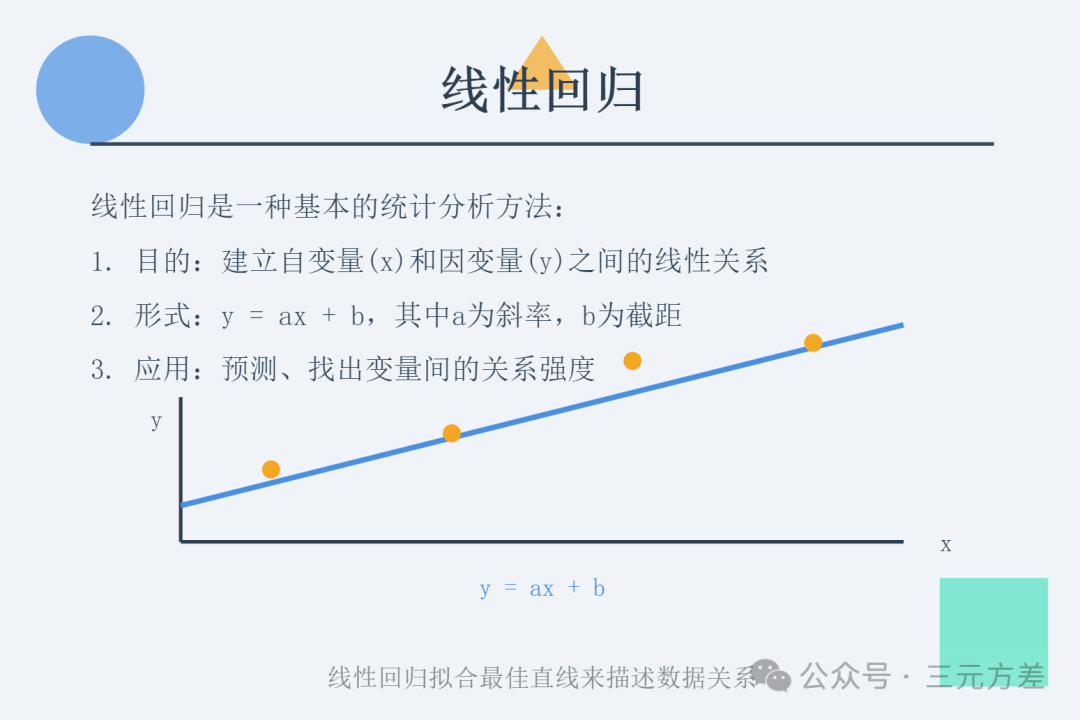
线性回归的基本形式可以表示为：
Y = aX + b
其中：
Y 是因变量（我们想要预测的变量）
X 是自变量（用来预测Y的变量）
b 是Y轴截距
a 是斜率
举一个简单的商业案例，比如：
假设一家咖啡连锁店想了解广告支出（X）与销售额（Y）之间的关系。收集了过去12个月的数据后，使用线性回归分析得出以下结果：
Y = 50,000 + 5X
这个方程告诉我们：
即使不投放广告，基础销售额也有50,000元（b = 50,000）
每增加1元广告支出，预期可以带来5元的销售额增长（a = 5）
斜率的符号和大小都很重要：
正号表示正相关：发帖数越多，在线时间越长。
负号表示负相关：如果是-5，就意味着每多发一个帖子，在线时间反而减少5分钟。
系数的绝对值大小反映了影响程度。例如，0.5比5的影响小得多。
除了回归方程，回归分析通常还会输出以下重要信息：
R²：决定系数，表示自变量对因变量变异的解释程度。
R方值是一个介于0和1之间的数值，反映模型的解释力：
R方 = 0.8，意味着80%的在线时长变化可以用发帖数来解释。这是个不错的模型！
R方 = 0.2，则说明只有20%的变化可以解释，可能还有其他重要因素我们没有考虑到。
注意：R方值过高（如0.99）可能意味着模型过拟合或变量间存在某种必然的数学关系。
1.1 最小二乘法：画线的艺术
线性回归的核心任务是在散点中找到一条最能代表整体趋势的直线，即"回归线"。
但如何确定这条线的位置呢？
这就要用到"最小二乘法"。其原理是：找到一条线，使所有数据点到这条线的垂直距离的平方和最小。我们使用平方和而不是简单的距离和，是为了：
避免正负距离相互抵消
对离群点施加更大的"惩罚"，使回归线不易受极端值影响
虽然原理听起来复杂，但现代统计软件已经为我们简化了这个过程。比如excel可以直接添加趋势线和公式，我们的任务是解读结果，并从中获取商业洞察。
2. 多元回归
在商业分析中，我们常常发现单一因素无法充分解释复杂的现象。
例如，用户的在线时长可能不仅与发帖数有关，还可能受年龄、职业、甚至天气等因素的影响。
面对这种情况多元回归应运而生，它允许我们同时考虑多个因素的影响。
2.1 从单因素到多因素
想象你正在分析影响房价的因素。
起初，你可能只考虑房屋面积：房价 = a0 + a1 * 面积 + b
但很快你意识到，这个模型过于简化。地理位置、房龄、周边设施等因素都可能影响房价。
于是，你的模型演变为：房价 = a0 + a1 * 面积 + a2 * 地理位置 + a3 * 房龄 + a4 * 周边设施 + b
这就是多元回归模型的基本形式。
2.2 多元回归的应用
让我们通过一个实际案例来深入理解多元回归的应用。
某电商平台希望提高其转化率（即浏览到购买的比率）。他们收集了以下数据：
页面停留时间（分钟）
商品展示位置（1-10，1为最靠前）
用户过去一个月的购买次数
商品折扣力度（%）
用户性别（0为女性，1为男性）
经过多元回归分析，他们得到了如下模型：
转化率 = 0.02 + 0.005 * 停留时间 - 0.01 * 展示位置 + 0.02 * 购买次数 + 0.001 * 折扣力度 + 0.005 * 性别
解读这个模型，我们可以得出以下洞察：
页面停留时间：每多停留1分钟，转化率平均增加0.5个百分点。这表明提高页面吸引力和用户体验可能会带来显著收益。
商品展示位置：位置每提前一位，转化率平均提高1个百分点。这证实了"黄金位置"的重要性。
过往购买次数：每多一次过往购买，转化率平均提高2个百分点。这强调了客户忠诚度的价值。
折扣力度：出人意料的是，折扣对转化率的影响相对较小。每增加1%的折扣，转化率仅提高0.1个百分点。
用户性别：男性用户的转化率平均比女性高0.5个百分点，但这种差异相对较小。
基于这些发现，电商平台可以制定更有针对性的策略：
优化页面设计，增加用户停留时间。
精心设计商品展示顺序，将重点商品放在前列。
加强客户关系管理，鼓励重复购买。
重新考虑折扣策略，可能需要结合其他促销手段。
考虑针对不同性别的个性化营销，但不必过分强调性别差异。
·END·
看完觉得写得好的，不防打赏一元，以支持蓝海情报网揭秘更多好的项目。
感谢您的支持，我会继续努力的!
打开支付宝扫一扫，即可进行扫码打赏哦
手机直接保存图片,扫一扫识别二维码,即可进行扫码打赏哦
